by Andrew Kliman
A few months ago, I published “Henryk Grossmann’s Breakdown Model: On the Real Cause of the Fictitious Breakdown Tendency,” in With Sober Senses. In some quarters, the response to it has been quite favorable. I have also received some challenges to my arguments and conclusions, as well as some questions. Below, I respond to the latter. My main conclusion remains unchanged: “the Bauer-Grossmann reproduction scheme and the theory of breakdown and crisis derived from it are irreparably flawed.”
To respect the desire for anonymity, I have not attributed the challenges and questions that appear below to any individual, but they are actual feedback, sent to me by e-mail. I have edited them, mostly for the purposes of providing context and making their import clearer to readers.
Challenge #1: Your spreadsheet models employ arbitrary and questionable assumptions. For instance, they assume that the growth rate of physical means of production is constant. Why is this more plausible than Bauer and Grossmann’s assumption that the growth rate of the constant capital (in value terms) is constant? In addition, one model assumes a constant capital/output ratio, while the other assumes that the proportion of surplus-value that’s accumulated is constant. How different in principle is the latter, especially, from Bauer and Grossmann’s assumption of constant rates of accumulation of constant and variable capital? And your spreadsheets allow for the devaluation of constant capital but not the devaluation of variable capital, but both are features of the real world; devaluation of variable capital implies a rising endogenous rate of surplus-value but you ignore that, too.
Response: Prior to discussing the spreadsheet examples, I noted, “The results of the preceding analysis are general. They pertain to all cases––all growth paths of circulating constant capital, new value, and the total value of output––other than the IC [implausible cases, i.e., the case in which physical output is constrained to grow more slowly than productive demand and the case in which total profit is less than new productive investment]” (emphases added).
So the spreadsheet examples are just that––examples. They are not models, because I do not attempt to infer any general results from them. None of the theoretical conclusions arrived at earlier in the article, such as the disappearance of Grossmann’s breakdown tendency, depend in any way on the special assumptions of the spreadsheet examples. So alter these special assumptions however you wish and construct a new spreadsheet example on their basis. If your assumptions are internally consistent, don’t violate Marx’s value theory (i.e., equation (7) of my article), and don’t implicitly or explicitly assume an IC, there will be no Grossmann-style breakdown.
Challenge #2: You write that, while Grossmann’s breakdown condition is a situation in which there’s not enough supply in relation to productive demand, economic “slumps in capitalism are situations in which there’s not enough demand in relation to supply.” This is analysis at the level of circulation, not production.
Response: It isn’t analysis at all, just observation of a phenomenon. I warned against construing the statement as an explanation instead of as an observation: “capitalist slumps … are characterized by (but not, in my view, caused by) sluggish demand, not by demand that grows ever more rapidly.” My point in that section is simply that one first has to get the phenomenon right before one can hope to explain it properly.
Challenge #3: You say that Grossmann’s breakdown tendency stems in part from his assumption that the growth of productive demand is determined exogenously, outside his model. You criticize this, writing that “the growth of productive demand is determined endogenously, not exogenously, and its key determinant is the share of surplus-value (profit) that capitalists invest in production.” This seems suspiciously close to Say’s Law––the dictum that “supply creates its own demand” and, therefore, that general overproduction of commodities and economy-wide recessions are impossible.
Response: That’s funny; I’ve always thought that capitalists’ ability to hoard some profit, invest it in financial instruments, etc., instead of investing it in production (or using it to buy other goods and services) is the antithesis of Say’s Law. As Marx argued:
Nothing can be more childish than the dogma, that because every sale is a purchase, and every purchase a sale, therefore the circulation of commodities necessarily implies an equilibrium of sales and purchases. … its real purport is to prove that every seller brings his buyer to market with him. Nothing of the kind. … no one is forthwith bound to purchase, because he has just sold. If the interval in time between the two complementary phases of the complete metamorphosis of a commodity become too great, if the split between the sale and the purchase become too pronounced, the intimate connexion between them, their oneness, asserts itself by producing—a crisis.
Challenge #4: You write that, “in Marx’s theory, the immediate causes of economic slumps are financial crises.” Where does Marx state that this is always the case?
Response: As far as I know, he didn’t. But it’s not a fair question, because I said nothing about “always” here, and I didn’t even say that this is what he stated. My statement is about the character of the theory (specifically, the immediate causes of slumps within the theory), which is not necessarily the same thing. I stand by what I wrote.
There may be cases in which theorists (Marxist and non-Marxist) of crisis theorize about what must always happen, but that’s rather rare, if it occurs at all. Marx’s crisis theory refrains from such stuff (except in the context of “if … then” statements, of course), if I recall correctly.
Challenge #5: You note that, in the first stage of his analysis, Grossmann argued that technological change causes constant capital to grow more rapidly than new value. Then, in the second stage of his analysis, he argued that “technological change also generates a ‘modifying countertendency’: it cheapens commodities, including the means of production, and this retards the growth of constant capital.” You claim that “[t]his two-step method of dealing with the effects of a single cause is rather unusual.” But Marx identified the “Cheapening of the Elements of Constant Capital” as a countertendency, too, and he did not include it in his reproduction schemas or initial discussion of tendency for the rate of profit to fall.
Response: Yes, I know. But it’s unusual to do that. And because it’s unusual, it’s not surprising to learn that lots of people object to it, which was my point.
Please note that my article doesn’t criticize Grossmann’s two-step method as such. (“In my view, the real problem is not so much that he split his investigation into two stages, ….”) It criticizes the fact that the second-step consideration of the cheapening of commodities was based on intuition rather than analysis. Grossmann failed to work out “the precise amount by which commodities’ values fall in response to technological change,” but knowledge of the precise amount is needed in order to properly assess the effects of the cheapening of commodities. In particular, it is needed in order to determine whether the cheapening of commodities merely postpones the moment of breakdown––as Grossmann claimed, incorrectly––or whether it eliminates the breakdown tendency entirely––which is the actual result, as I showed.
Challenge #6: You criticize Grossmann for relying on intuition. You write that he actually didn’t know what he stated: “How did he [Grossmann] know that values do not fall to such an extent that circulating constant capital grows at the same rate as new value and the total value of output, instead of at a greater rate?” But the point of Bauer and Grossmann’s model, following Marx’s “intuition,” is that the organic composition of capital rises, which leads the rate of profit to fall.
Response: It is plain incorrect, demonstrably incorrect, to allege that Marx’s arguments about the rising organic composition of capital and the consequent falling rate of profit were based merely on intuition, in the same sense that Grossmann’s postpone-but-not-eliminate-breakdown conclusion was based merely on intuition. And if “the organic composition of capital rises, which leads the rate of profit to fall” were indeed “their point”––if “their point” did not, in addition, go to the question of whether the mass of profit is sufficient to allow capital to accumulate at the postulated rate, and thus the question of breakdown––then Grossmann would be long forgotten, I wouldn’t have written my article, and we wouldn’t be having this discussion.
Challenge #7: Your article points out that Bauer and Grossmann “stipulate[e] the growth rate of circulating constant capital in advance––in other words, assum[e] that its growth is exogenously determined.” You say that this is “incompatible with the theory [Marx’s value theory]. … [T]he theory does not allow one to stipulate the growth rate of constant capital in advance.” But it depends on the purpose of the model. For Bauer, the purpose was to demonstrate that capitalist accumulation could occur at a given rate indefinitely. Grossmann recognized that the model proved the opposite: that accumulation could not take place at any given rate indefinitely, given a rising organic composition of capital and falling rate of profit. This is a valuable conclusion.
Response: No, it doesn’t depend at all on the purpose of the model. It’s simply a fact that it is incompatible with Marx’s value theory to assume that the growth of circulating constant capital is determined exogenously. The theory says that the growth of circulating constant capital is determined endogenously, i.e., within the valuation process.
The reason it is determined endogenously is that, as I pointed out,
constant capital is an amount of value. The growth rate of circulating constant capital in value (or price) terms therefore depends not only on the growth rate of physical means of production; it also depends on the price of these means of production. Their price changes over time, in response to rising productivity and other factors, and one function of the value theory is to tell us the amount by which it changes.
Please note that my argument here is not about whether it is permissible for someone to assume that the growth of circulating constant capital is determined exogenously, nor about whether someone who makes that assumption is “a Marxist” or any such rot. It’s about what is and isn’t compatible with the value theory.
Please note also that I’m not arguing that a constant growth rate of constant capital is always incompatible with Marx’s value theory. If one assumes that the growth rate of physical means of production is constant, and if one also assumes that there are no changes in productivity or in other things that tend to cause per-unit prices to change, one has in effect assumed a case in which (according to Marx’s value theory) the growth rate of constant capital is constant. In such a case, a constant growth rate of constant capital is compatible with the value theory.
But Bauer and Grossmann were considering a case in which there are continuous increases in productivity. And when productivity increases, Marx’s value theory says that the prices of commodities––including means of production––tend to decline. It also says that the decline in prices necessarily reduces the growth of circulating constant capital in value (or price) terms. It is therefore incompatible with the theory to assume both a constant growth rate of constant capital and rising productivity.
My point here is basically the same point that Grossmann made when he charged Bauer with having produced a self-contradictory model. It’s okay to assume that constant capital grows at a constant rate. And it’s okay to assume technological advances that cause productivity to increase. But assuming both things at the same time is self-contradictory (or at least incompatible with Marx’s value theory).
Challenge #8: You say that the breakdown tendency disappears once the value of constant capital is determined endogenously. And you say this conclusion “hold[s] true in cases that conform to the spirit of the Bauer-Grossmann reproduction schemes: that is, cases in which physical means of production permanently increase at one rate while employment of workers and generation of new value increase at a lower rate.” But contrary to your assertion, Bauer and Grossmann didn’t assume only that physical means of production increase at one rate while employment increases at a lower rate. Unlike you, they also assumed that the value of constant capital permanently grows faster than the new value created by workers.
Response: Yes, Bauer and Grossmann assumed both things. In my article, I noted that fact several times.
However, as Grossmann pointed out, it is untenable to assume that physical and value magnitudes grow at the same rate when productivity is rising. Because rising productivity cheapens commodities, constant capital (in terms of value) has to grow more slowly than physical means of production. The “contradiction” in Bauer’s model that Grossmann identified (constant per-unit values despite rising productivity) can’t be resolved without jettisoning the equality of the growth rates of means of production and constant capital. One or the other must change. (Grossmann understood this clearly. He said that the growth of constant capital––in terms of value–is reduced.)
So a proper theorization of the matter—one that eliminates the “contradiction” in Bauer’s model–cannot conform to the letter of the model. At most, it can conform to its spirit.
The question then arises, what is the spirit of the original Bauer model? I.e., what was he trying to do that can still be done without falling into self-contradiction? He was trying to model labor-saving technical change. Thus, as I noted, “when Bauer assumed that constant capital grows at 10% per annum while new value increases by only 5%, his clear intention was to model a process of technological change in which physical means of production increase by 10% per annum while employment increases by 5%.” My spreadsheet examples use the exact same growth rates. They thereby conform to the spirit (though not the letter, of course) of Bauer’s model.
Challenge #9: You say that “[t]he Bauer-Grossmann scheme of reproduction abstracts from fixed capital.” But Bauer and Grossmann do not make the distinction between fixed and circulating constant capital in their schemas, i.e., abstract from fixed capital. They simply assume that fixed capital turns over annually. Grossmann was explicit. A few paragraphs below his Table 2.4, he wrote: “The reproduction scheme has so far assumed, for the sake of simplification, that the life cycle of fixed capital equals one period of reproduction; that fixed capital is completely used up in each cycle of production and therefore has to be renewed from the year’s product.”
Response: The quotation from Grossmann isn’t dispositive. He’s entitled to use technical terms in the manner he wishes, but so am I, and so is Marx. I spelled out what I meant in the remainder of the paragraph from which you quote. And near the start of his analysis of simple reproduction, Marx wrote the following:
the materials of production are entirely consumed and their values completely transferred to the product. But only a portion of the employed fixed capital is wholly consumed and its value thus transferred to the product. Another part of the fixed capital, such as machines, buildings, etc., continues to exist and function the same as before, though depreciated to the extent of the annual wear and tear.
Given this usage of fixed capital, there isn’t any fixed capital in the Bauer-Grossmann model, since there isn’t any capital that “continues to exist and function the same as before.” Equivalently, it’s not the case that “only a portion of” what Grossmann calls fixed capital “is wholly consumed.”
This doesn’t mean that Grossmann’s usage of fixed capital was wrong. I understand what he meant––in addition to raw materials and such, the material elements of the constant capital include machines, tools, buildings, etc.; but in contrast to most machines, tools, buildings, etc., these ones are wholly consumed with a year, and so their value is transferred to the year’s physical product.
In the context of my article, what to call the constant capital is a distraction that has no bearing whatsoever on the analysis or the results. What matters is not the terminology, but the rate of growth of the constant capital that circulates annually (whatever one calls it). I show that Marx’s value theory implies that, in the limit, the constant capital that circulates annually grows at the same rate as new value and the total value of output, instead of at a greater rate. Consequently, the long-run breakdown tendency is eliminated.
Challenge #10: You write that Grossmann’s “discussion of capitalist production and reproduction focused on their value dimension while giving short shrift to, if not actually ignoring, their use-value (physical) dimension.” But Marx’s reproduction schemas are likewise focused on the value aspect of production and reproduction, not the use-value aspect.
Response: I disagree. Because Marx’s schemes abstract from technological change, their per-unit values remain constant over time. Consequently, the value magnitudes and their movements perfectly reflect physical magnitudes and their movements. (E.g., if the constant capital, in terms of value, increases by 10%, from 200 to 220, and the per-unit price or value of means of production remains constant at 10, then we know that the physical means of production have also increased by 10%, from 200/10 = 20 to 220/10 = 22.) So, simply by telling us that per-unit values are constant, Marx provided all of the information we need regarding the physical figures and their movements.
For the same reason, Bauer and Grossmann didn’t need to provide explicit physical figures for their scheme. But once Grossmann (correctly) dropped the assumption that per-unit values are constant despite technical change, then more information about physical quantities became necessary. If we want to know the amount by which constant capital changes, in value terms, we need to know the amount of change in the physical amount of means of production, and the amount of change in the per-unit value. And to know the amount of change in a commodity’s per-unit value, we need to know more than the total value of the output of the industry that produced the commodity. We also need to know how much physical output it produced.
In Marx’s schemes, the analysis of what’s happening to the values is at the same time an analysis of what’s happening to the use-values––because, again, the value magnitudes and their movements perfectly reflect physical magnitudes and their movements. Thus, he says, correctly, that (simple) reproduction “is not only a replacement of value, but also a replacement in material and is therefore as much bound up with the relative proportions of the value-components of the total social product as with their use-value, their material shape” (emphases added). In the same paragraph, he stresses that, when dealing with reproduction, it is no longer appropriate to abstract from the specific use-values that contain the value.
Indeed, the whole design of the schemes—two departments, etc.—is based on there being two fundamentally different kinds of use-values that are relevant, and on the necessity of renewing them in specific amounts, and on the necessity of allocating them in specific ways. The last issue, correct allocation of use-values, is why the exchanges between departments, and the intra-department “exchanges,” are so important to his analysis. And indeed, the quantities of the use-values and their “destinations” are very important in terms of the overriding purpose of Marx’s schemes and analysis of reproduction—disproving Adam Smith’s trickle-down dogma that all accumulated capital ultimately accrues to the working class (see p. 46 of my paper on the reproduction schemes). Simply put, workers don’t eat machines, so there ain’t no way that surplus-value accumulated in the form of machines ever resolves into additional variable capital.
Finally, although Marx sometimes discussed reproduction in value terms, his core definitions of simple and expanded reproduction are physical. For instance, he noted that if means of production and subsistence become cheaper, expanded reproduction can occur without an increase in the sum of value advanced. And if means of production and subsistence become more expensive, then reproduction might contract, not expand, even though capital increases in terms of value:
In P … P the new circuit may be started by P with the same or perhaps even a smaller value and yet may represent a reproduction on an extended scale, for instance when certain elements of commodities become cheaper on account of increased productivity of labour. Vice versa, a productive capital which has increased in value may, in a contrary case, represent reproduction on a materially contracted scale as for instance when elements of production have become dearer. The same is true of C’ … C’.[1]
Challenge #11: You write, “Movements in value magnitudes cannot, therefore, be properly explained when one abstracts from, or fails to investigate, what is taking place in terms of use-value.” So either Marx got it wrong in his reproduction schemas in Capital 2 or Grossmann’s reproduction schema and subsequent discussion of their use value aspects is ok?
Response: No, Marx didn’t abstract from or fail to investigate what is taking place in terms of use-value. As I explained in my response to Challenge #10, his schemes held per-unit prices (or values) constant. By telling us this, he provided all of the information we need regarding what is taking place in terms of use-value. For example, if one of his value magnitudes increases by x%, we immediately know that the associated physical magnitude has likewise increased by x%.
As I also explained in that response, Grossmann didn’t need to provide explicit physical figures for his reproduction scheme, because it, too, assumes that the per-unit price or value of the commodity remains constant. What was ok about this was stating that it remains constant and then not saying more about physical quantities, because he has already told us all we need to know about them. What wasn’t ok (as he recognized) is the assumption that the price or value of the commodity remains constant even though productivity continually increases.
Once Grossmann dropped that assumption, he should have provided us––and himself––with much more information about physical quantities, the commodity’s price or value, and their movements. But he didn’t do so. He just offered generalities, such as statements that the value falls and that this retards the growth of constant capital (in value terms). Since he failed to specify what was taking place physically, he didn’t know more than these generalities.
Yet these generalities were woefully insufficient to do the work he tried to make them do. He took the generality that the growth of constant capital slows down, and then used his intuition to conclude that the breakdown tendency is still present; the moment of breakdown is postponed, but not eliminated.
His intuition was wrong. His statements that the breakdown tendency still exists were therefore wrong as well. And it was wrong of him to assert as fact something that he intuited but did not actually know. None of that is ok.
As I explained in my article, the generality that the growth of constant capital slows down doesn’t tell us, and didn’t tell Grossmann, the amount by which it slows down. (To know the amount of slowdown, he needed information that he didn’t have, regarding the amount by which physical means of production increase, and regarding the amount by which their price or value falls.) If the growth of constant capital slows down to such a point that constant capital does not grow more rapidly than the total value of output, then the moment of breakdown is indeed eliminated, not merely postponed.
And that’s exactly what Marx’s value theory implies, as my article demonstrates. In the limit, circulating constant capital and the value of output grow at the same rate. There is no Grossmann-style breakdown or tendency toward breakdown.
Challenge #12: Nowhere does Marx present anything like your hybrid use value/value schema.
Response: Au contraire, mon frère. There are numerous places in which Marx employs what you call a “hybrid use value/value schema.” That is, there are numerous places in which he uses physical quantities and per-unit prices or values to compute value magnitudes (e.g., the value of corn is £2 per quarter and 100 quarters of corn are produced, so their total value is £200).
It is true that Marx’s reproduction schemes don’t contain explicit figures for physical quantities, just figures for value magnitudes. But that is because, as I have discussed in my responses to Challenges ##10-11, his schemes held per-unit prices (or values) constant. The value magnitudes of his schemes, and their movements, therefore perfectly reflect physical magnitudes and their movements. By telling us that the per-unit prices or values are constant, Marx gave us all the information we need regarding movements in the physical quantities underlying the schemes.
But elsewhere, Marx certainly does use physical quantities and per-unit prices (or values) to compute value magnitudes. One extremely prominent example of this is Chapter 7 of Capital, volume 1. I’ll quote just a small part of this “hybrid use value/value schema”:
Let us now examine production as a creation of value.
… Assuming this product to be 10 lbs. of yarn,
… For spinning the yarn, raw material is required; suppose in this case 10 lbs. of cotton. … our capitalist has, we will assume, bought it at its full value, say of ten shillings. … the wear and tear of the spindle, … amounts to the value of 2s. If, then, twenty-four hours’ labour, or two working-days, are required to produce the quantity of gold represented by twelve shillings, we have here, to begin with, two days’ labour already incorporated in the yarn.
… The values of the means of production, i. e., the cotton and the spindle, which values are expressed in the price of twelve shillings, are therefore constituent parts of the value of the yarn, or, in other words, of the value of the product.
… If in one hour 1 2/3 lbs. of cotton can be spun into 1 2/3 lbs. of yarn, then 10 lbs. of yarn indicate the absorption of 6 hours’ labour.
… the value of a day’s labour-power is three shillings, … six hours’ labour is incorporated in that sum; and consequently … this amount of labour is requisite to produce the necessaries of life daily required on an average by the labourer. If now our spinner by working for one hour, can convert 1 2/3 lbs. of cotton into 1 2/3 lbs. of yarn, it follows that in six hours he will convert 10 lbs. of cotton into 10 lbs. of yarn. Hence, during the spinning process, the cotton absorbs six hours’ labour. The same quantity of labour is also embodied in a piece of gold of the value of three shillings. Consequently by the mere labour of spinning, a value of three shillings is added to the cotton.
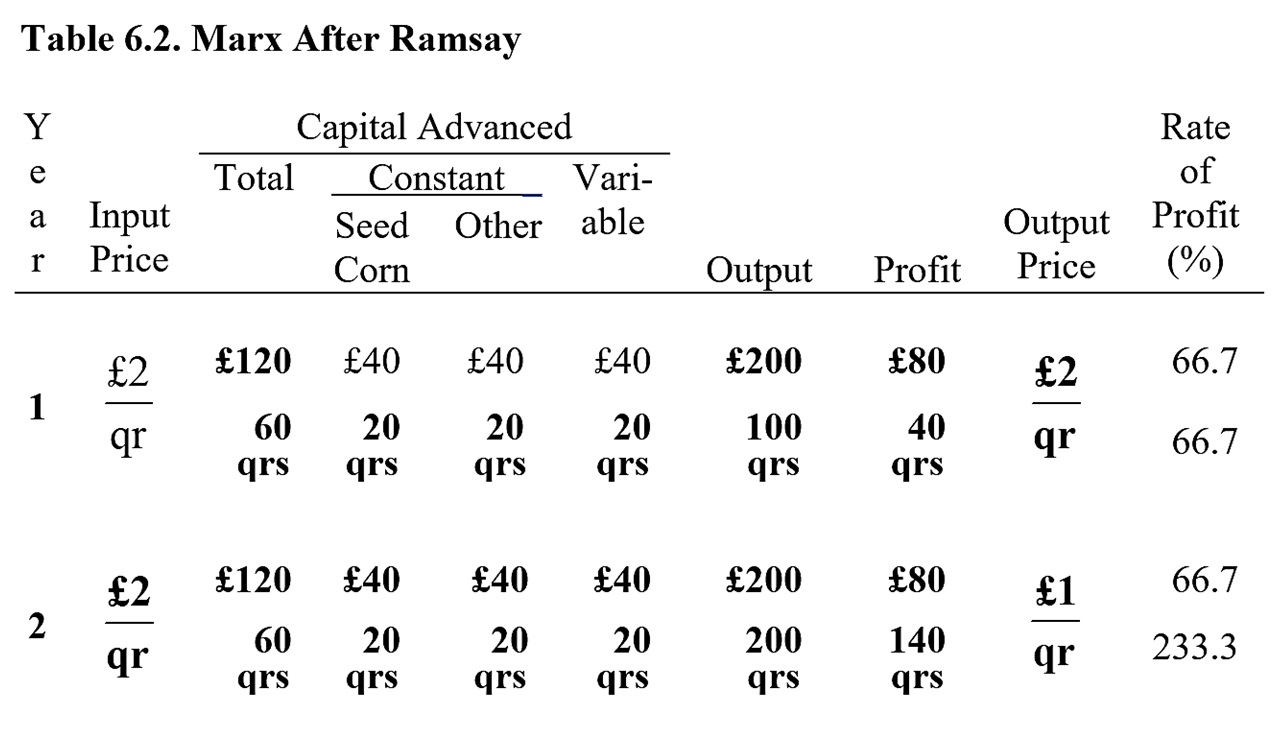
I discussed another “hybrid use value/value schema” of Marx’s, contained in his “Economic Manuscript of 1861–63” (Marx-Engels Collected Works, vol. 33, pp. 266ff), in my book Reclaiming Marx’s “Capital.” Table 6.2, which appears on page 102 of my book and is reproduced below, summarizes Marx’s computations. All figures in boldface are Marx’s own; the others are inferred from the context.
The use of physical quantities and per-unit prices to compute value magnitudes is sound procedure. If one fails to employ it, and instead arbitrarily imposes conditions like “constant capital grows by 10% per year; new value grows by 5% per year”––while failing to consider how these conditions affect the associated physical variables––one opens the door to all manner of absurd or even impossible situations. For example, the Bauer-Grossmann reproduction scheme implies that the amount of physical output invested in next year’s production is eventually more than the total amount of physical output that has been produced (where does the extra amount come from?); that capitalists eventually invest more than their total profit (where does the extra investment funding come from?); that physical output always grows more slowly than physical productive demand; and that, eventually, just a tad less than 20 bushels of seed corn are needed, as input, to produce 20 bushels of corn output.
Question 13: You showed that the Bauer-Grossmann model implies that
the amount of seed corn needed to produce a bushel of corn output rises and rises. By year 65, the “capital/output” ratio exceeds 0.95, which means that, to produce 20 bushels of corn output, more than 19 bushels of seed corn are needed. And the “capital/output” ratio then moves even closer to 1 thereafter, so that production of 20 bushels of corn output eventually requires just a tad less than 20 bushels of seed com as input. It is hard to call this pattern of technological change “progress.”
But in value terms, isn’t this precisely what the rising organic composition of capital means?
Response: I don’t understand the question. What is the value counterpart of “production of 20 bushels of corn output eventually requires just a tad less than 20 bushels of seed com as input”? I think the question may be based on confusion of one relation, the relation between means of production and output, with a different relation, the relation between means of production and the wages and benefits workers receive. The so-called “capital/output” ratio is a relation between (physical) means of production and (physical) output, while the organic composition of capital is a relation between the price or value of means of production and the amount of value paid to workers.
Question 14: The movement of the commodity’s per-unit price (or value) is a crucial variable in your analysis. But what determines its movement? The economic (as opposed to mathematical) logic of the equations used to govern its decline are unexplained.
Response: The mystery economic logic is that (a) the total value of the product is the sum of the value transferred from used-up means of production and the new value created by living labor; (b) the value per physical unit is the total value of the product divided by the number of physical units produced; and (c) the price per physical unit equals the value per physical unit when only one good is produced.
Question 15: The political rationale for your article is that Grossmann is invoked by “radicals whose outlook is fatalist and whose politics are informed by fatalism.” You provide one example, Michael Roberts. What evidence do we have that his politics are informed by fatalism? And are there others like him?
Response: My article quotes his statement that “capitalism cannot continue indefinitely … but must reach its limits as a system of social organisation, then break down and be replaced by a new system.” It also quotes his statement that “[c]apitalism then heads for breakdown and the final confrontation with the working class. It’s socialism or barbarism.” These are political statements, and they are informed by fatalism.
There are definitely others. Roberts is not a lone wolf; he has a pack of devotees.
In addition, about a decade ago, I received a draft essay, written by someone other than Roberts. In the introduction, the author wrote,
social relations will only be changed when the current one[ ] becomes a fetter on the development of the productive forces. The question I am asking in this essay is whether Marx’s critique of political economy reveals to us that capitalism necessarily becomes such a fetter. I am asking this because on that question hinges the necessity of socialist revolution. …
Grossman answered affirmatively [… that] Marx’s writings on political economy reveal that capitalism necessarily becomes a fetter on the development of the productive power of human society. I agree with writers such as Kuhn, Yaffe, [and] Mattick who have argued that Grossman … correctly interpreted Marx’s theory of breakdown (collapse) and crises.
And consider the following screed, written by Guglielmo Carchedi (together with Roberts) for the underconsumptionists/Stalinists at Monthly Review:
Some Marxist authors, even though severe critics of Heinrich in many other respects, have accepted Heinrich’s position that the law cannot predict the inevitability of the fall of the ROP [rate of profit] in the future. For example, … Kliman et al. …
[This] is disastrous for labour’s struggle against capital. If we cannot predict the inevitability of the tendential fall in rate of profit and thus of crises, we deprive labour’s fight of its objective ground, the recurrent attempt by the system to supersede itself due to its internal contradictions. Labour’s fight, then, rather than being the conscious manifestation of the system’s blind force of self-destruction, becomes a purely voluntaristic act.
Kliman and his co-authors’ … position is harmful for the working class and its fight against capital.
(The irrationality and mean-spiritedness of this rant are rivaled only by its idiocy and thoughtlessness. If the weather forecast says that it is very likely to rain, this is certainly no prediction that rainfall is inevitable, but my grabbing an umbrella just isn’t a “purely voluntaristic act” that lacks any “objective ground.”)
ENDNOTE
[1] P is Marx’s symbol for productive capital––i.e., capital that exists in the form of elements of physical production (means of production and labor-power). P … P is his notation for the circuit of productive capital, in which capital in the form of elements of physical production is transformed into capital held in the form of physical output, and then into capital in money form, and finally back into capital in the form of elements of physical production. C’ is his symbol for commodity capital––i.e., capital held in the form of physical output. C’ … C’ is his notation for the circuit of commodity capital, in which commodity capital is the starting point and ending point of the circuit previously described.



Be the first to comment